Researchers have made a breakthrough in the ability to solve engineering problems.
In a new paper published in Nature entitled, “A scalable framework for learning the geometry-dependent solution operators of partial differential equations”, they explain the current challenges in solving partial differential equations.
Partial Differential Equations are a specific type of equation where it is usually impossible to write down a specific formula for the solution. There are ways to “almost” solve them through many complex mathematical techniques that approximate the answers.
Partial differential equations are frequently used in engineering and medical applications. Wikipedia lists some applications:
“For instance, they are foundational in the modern scientific understanding of sound, heat, diffusion, electrostatics, electrodynamics, thermodynamics, fluid dynamics, elasticity, general relativity, and quantum mechanics (Schrödinger equation, Pauli equation, etc.). They also arise from many purely mathematical considerations, such as differential geometry and the calculus of variations; among other notable applications, they are the fundamental tool in the proof of the Poincaré conjecture from geometric topology.”
The problem is that the current methods of approximating the solutions typically require enormous amounts of computing power. This has limited the applications that make use of the equations.
The new research takes a different approach to solving partial differential equations: AI.
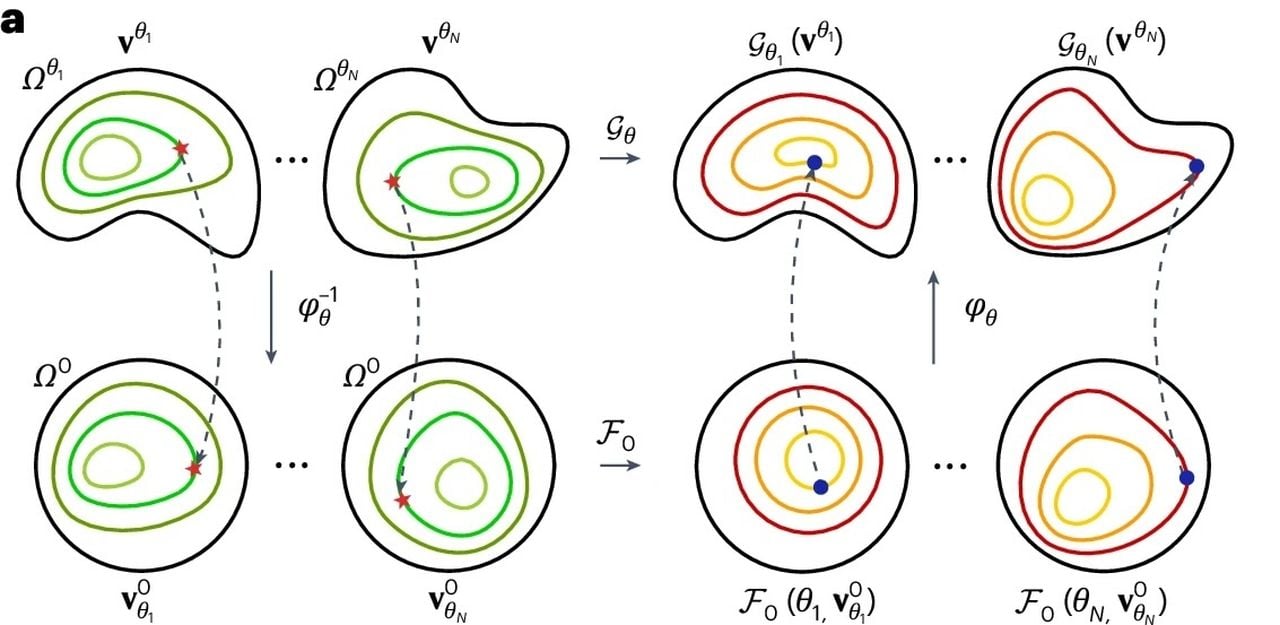
They developed a new AI framework called DIMON (Diffeomorphic Mapping Operator Learning) which attempts to solve these equations with far less computing capacity.
Neural networks have been used for this purpose in the past; however, they have typically been subject to significant constraints on geometry, making them less useful. The researchers explain DIMON:
“Here we aim to address the aforementioned computational challenges by proposing Diffeomorphic Mapping Operator Learning (DIMON), an operator learning framework that enables scalable geometry-dependent operator learning on a wide family of diffeomorphic domains. DIMON combines neural operators with diffeomorphic mappings between domains and shapes, formulating the learning problem on a unified reference domain (‘template’) Ω0, but with respect to a suitably modified PDE operator.”
Their training of DIMON seems to work, and it has resulted in a very significant performance advantage:
“At the inference stage, DIMON reduces the wall time needed for predicting the solution of a PDE on an unseen geometry by a factor of up to 10,000 with substantially less computational resources and high accuracy. In particular, the last example approximates functionals of PDE solutions (in fact, PDEs couple with a rather high-dimensional ordinary differential equations system) for determining electrical wave propagation on thousands of personalized heart digital twins, demonstrating its scalability and utility in learning on realistic 3D shapes and dynamics in precision medicine applications.”
How does this relate to 3D printing? It’s all about optimizing the design of parts. These days, that’s done with complex simulation tools that are expensive to operate. Usually, the amount of resources consumed is so high that very few iterations can be attempted, particularly on complex geometries.
If DIMON is commercialized, we may see implementations of 3D CAD tools that directly integrate simulation functions that operate far faster. It might then be possible for advanced part designs to be developed much more quickly, and by a wider audience that’s able to access the less expensive DIMON framework.
Via Nature
