
Thanks to the previous articles, we should have a pretty good understanding of the reasoning behind Computational Engineering and the fundamental technology necessary to support it.
Editor’s note: Lin Kayser has written a series of stories introducing the new concept of Computational Engineering being developed by his new company, Leap71. This is a six-part series, with links below to all parts as they are published:
Fundamentals of Computational Engineering: Prologue
Fundamentals of Computational Engineering: Part 1 — A Bit of History
Fundamentals of Computational Engineering: Part 2 — The Technology
Fundamentals of Computational Engineering: Part 3 — Voxels to the Rescue
Fundamentals of Computational Engineering: Part 4 Implicits
Fundamentals of Computational Engineering: Part 5 — All You Need is a Few Functions
Let’s talk about Tier 1, the geometry kernel, that supports the entire Computational Engineering software framework. As we discussed in the last article, it needs to be compact, robust, and fast.
There are a million ways to represent geometry in a computer. Most of them are vector based, using surface patches or triangles, to construct the shape of the object they are representing. Vectors are great for simple shapes, but they have a lot of drawbacks.
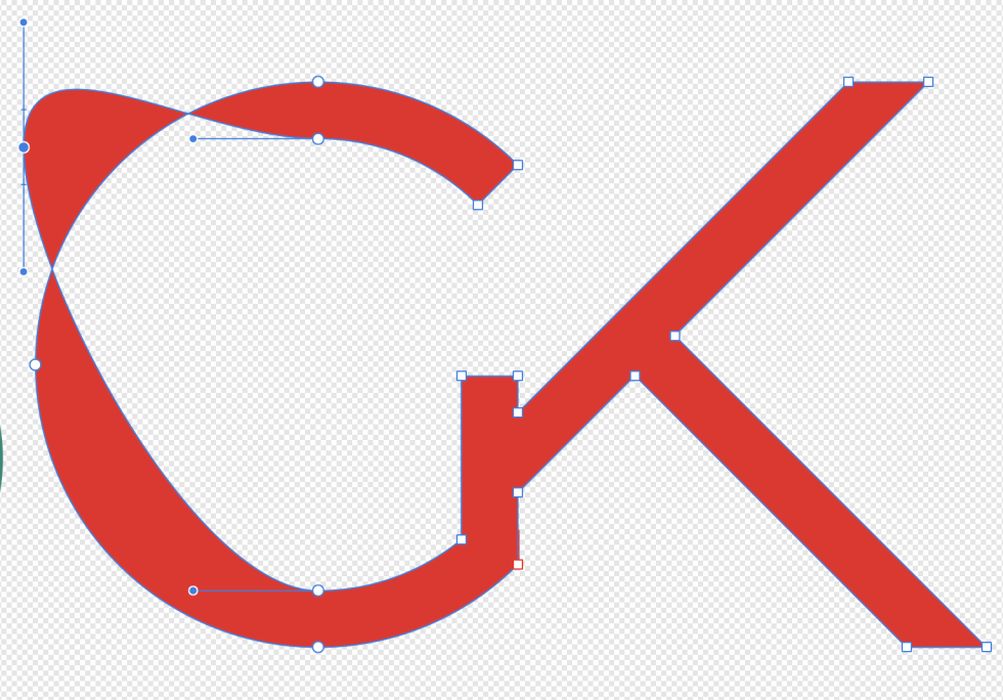
To simplify the thought process, let’s think in 2D for a second: Representing shapes with a vector outline, is a very flexible way to create simple geometry for, say, a logo. You can scale, rotate, and refine the control points to perfection.
For complex shapes, it’s a different story. Think of taking a picture of your surroundings with your camera. Would you represent this in a vector-based format? You could, but the resulting file would be much larger, and it would be next to impossible to manipulate. If you shift even small vectors around in a complex graphic, you can have surprising and non-localized effects that are hard to control.
The same is true for 3D geometry. Vectors are great for things like cubes, and Spline patches/NURBS are great for simple shapes, if your geometry gets complex, however, sophisticated mathematical representations of geometry become fragile, and it is very hard to create a consistent, robust setup that can be relied on.

So there is a reason why photos are stored as pixels. It’s easy to change a pixel. When you change one pixel, nothing else changes. It’s a very simple way to store an image that leaves no room for error.
So when we thought of the most robust representation of a complex physical part, my co-founder Michael Gallo suggested “why not just store all the atoms”.
Or, in other words, volumetric pixels: so-called voxels.
Voxels are points in space, on a 3D grid, that represent matter. For this initial discussion, let’s just say each voxel it is a cube in space that is either on or off, like the particle of a 3D printer being either there, or not. Think of the elements of a Rubik’s Cube. We will later dive into a more complex representation of a voxel, but for the general understanding how a geometry kernel works, this is sufficient for now.

Once something is rendered to voxels, it is robust, has no ambiguity, and can very easily be verified and understood. You can base subsequent operations on the rendered voxel geometry without fearing numerical instabilities later on. You have a single source of truth and a robust foundation. Nothing ever fails in voxel space.
The only drawback is, you have to pick the resolution, the number of volumetric elements, that represent your object. While a vector is mathematically “perfect”, voxels are “rough”. But so is the world: 3D Printers have a resolution, and other production methods have limited accuracy.
In the end, the world is composed of molecules — nothing is “infinitely smooth”.
As long as our resolution is high enough to provide the necessary fidelity for the production of the object, we will be fine. Just like a digital camera has more than enough pixels today for all practical purposes, and our eyes no-longer see the pixels on our screens.

A computationally engineered and then metal 3D-printed rocket injector head, created using a voxel paradigm by LEAP 71. Image source Aconity3D
Because voxels are so simple, they can also be made extremely fast, which means you can increase the resolution to the necessary level. At Hyperganic we had a long-time teammate, who followed me to every company I started, Michal Krcmar, who hand-coded machine-language optimizations for our code, to make it blazingly fast on modern processors. Very few people have that skill today, and he is one of them.
So, now we have the foundation of a a robust and fast geometry engine: a voxel-based data structure.
All the objects that my partner Josefine Lissner created in the past are based on this paradigm. It would have been next to impossible to model these complex parts using traditional geometry kernels. And this is just the beginning: These will be the least complex objects that you will see coming out in the coming years! And to state the obvious, each voxel can represent a different material, just like pixels can have different colors.

Almost a decade later, the choice of voxels for a computational geometry engine was the right one, and in the next articles, I will explain, why it is so powerful, and what operations are required to build a compact, robust kernel, that can be used by the Tier 2 high-level geometry-generating functions.
Editor’s note: Lin Kayser has written a series of stories introducing the new concept of Computational Engineering being developed by his new company, Leap71. This is a six-part series, with links below to all parts as they are published:
Fundamentals of Computational Engineering: Prologue
Fundamentals of Computational Engineering: Part 1 — A Bit of History
Fundamentals of Computational Engineering: Part 2 — The Technology
Fundamentals of Computational Engineering: Part 3 — Voxels to the Rescue
Fundamentals of Computational Engineering: Part 4 Implicits
Fundamentals of Computational Engineering: Part 5 — All You Need is a Few Functions
Via Leap 71
